TokenPocket是一款多功能的区块链钱包应用,支持多链和智能合约平台,为用户提供便捷的一站式数字资产管理服务。用户可以通过它管理加密货币资产、进行转账交易,并访问丰富的去中心化应用(DApp)和服务。确保助记词安全备份是保障资产安全的关键。
tp钱包TokenPocket是一个支持多链的区块链数字钱包,用户可以通过它来存储、管理和交易各种数字资产,包括比特币、以太坊等主流加密货币以及其他许多种类的代币。
它为用户提供了一个相对安全便捷的方式来持有他们的数字货币,并且可以进行交易、参与各种区块链应用(DApps)、以及进行区块链上的其他操作。
tp钱包通常采用多种安全措施,如多重签名、冷存储(将私钥离线保存)等,以保护用户的资产免受黑客攻击。
在实际的安装过程中,首先要下载tp钱包安卓版:
1. 首先,是安卓手机的安装,分各类手机品牌
(1) 华为手机:
在安装时允许继续安装。
不要将应用移入管控。
按照屏幕上的提示步骤完成安装。
(2) 小米手机:
在安装页面点击右上角设置。
开启安全守护。
返回并按提示完成安装。
(3) OPPO手机:
打开设置。
关闭所有软件的保护。
成功下载安装欧易App后再打开保护。
(4) 其他品牌安卓手机:
关闭网络和蓝牙。
使用夸克浏览器或手机自带的浏览器下载安装。
在设置中,将病毒检测改为360等,并信任此应用。
关闭数据流量再进行安装。
(5) 通用方法:
下载tp钱包安卓版直接安装
按照安装步骤安装即可
2. 对于苹果手机
直接在tp钱包的官方网站上下载安装。
请根据您的手机类型选择合适的下载方法,并按照上述步骤操作。在下载和安装过程中,确保遵循所有提示和指南以确保安装成功。如有安装不成功的,请及时联系我们,我们会竭诚为你服务!
tp钱包
tp钱包在技术创新方面也取得了显著成就,尤其在提供安全可靠的数字资产管理工具方面。它不仅支持与tp旗下的硬件钱包imkey配对,还提供了如Tokenlon这类支持「闪兑」功能的服务。
从2018年7月31日起,Tokenlon升级为独立的去中心化交易所(DEX),支持多种币种的自由交易。此外,tp钱包还支持多种DApp,包括金融、游戏、工具和社区类DApp,这些主要基于ETH和EOS公链。
使用tp钱包进行数字货币交易主要包括以下几个步骤:
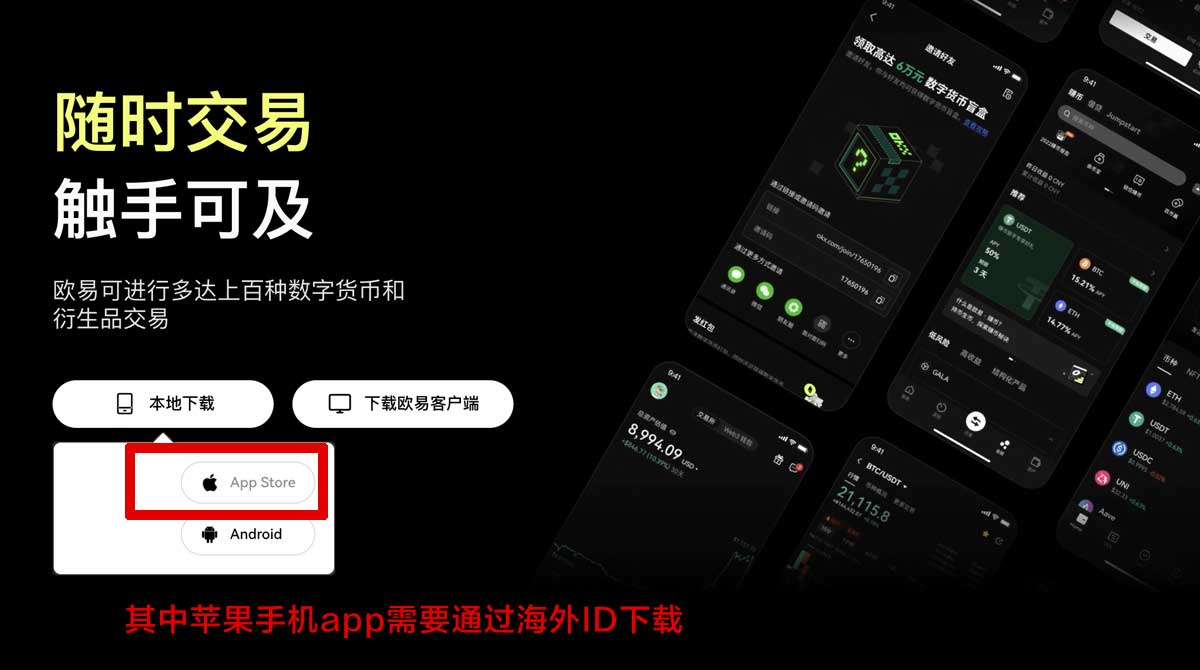
1.下载安装tp钱包:Android用户:可以在tp官网下载安装包进行安装。
iOS用户:由于中国内地Apple ID无法直接在App Store下载tp钱包,需要使用香港Apple ID进行下载安装。
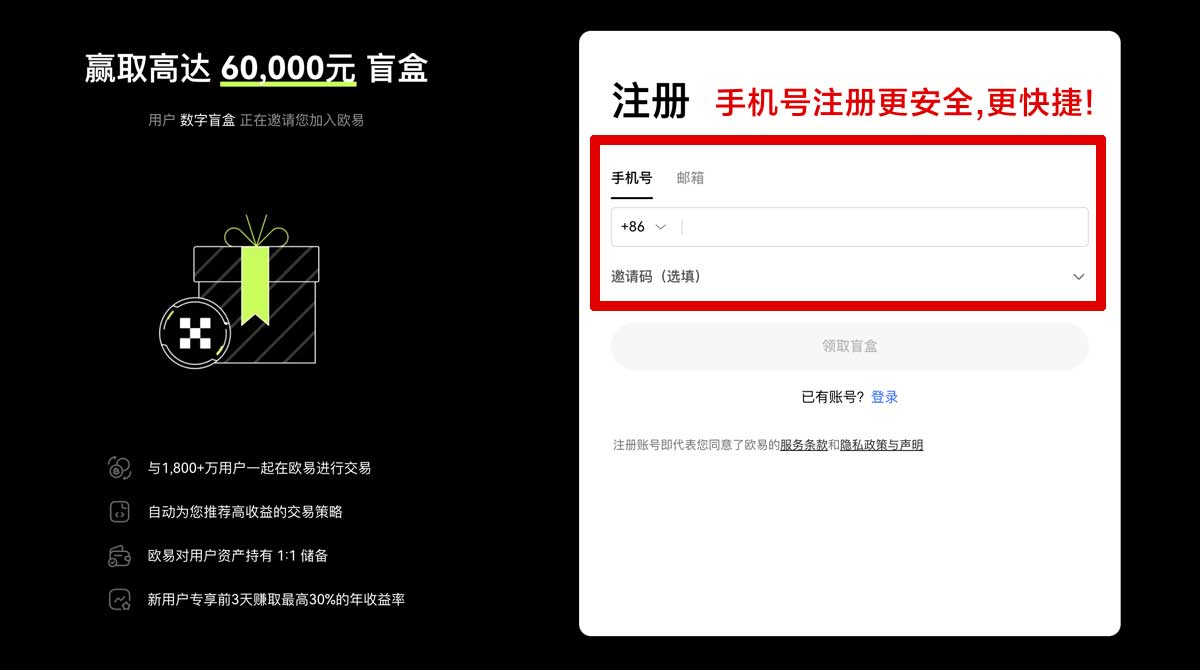
2.注册账号:打开tp官网进行注册,输入邮箱地址并验证。
进行手机号验证,设置账户密码。
完成注册后,进行身份认证以提高账户安全性。
3.交易前设置:添加收付款方式,如绑定银行卡、支付宝或微信支付。
进行KYC认证、绑定手机号和设置资金密码。
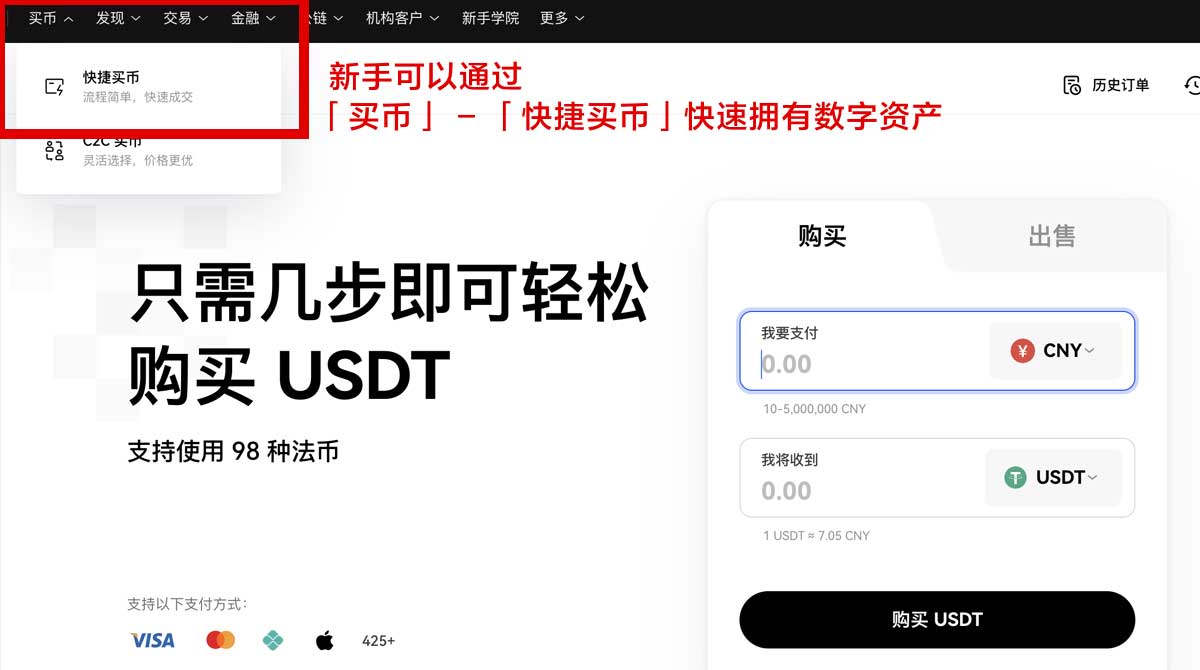
4.买币:在tp钱包中选择“买币”功能,可以选择快捷买卖或币币交易。
进行充值和资金划转,以便进行币币交易。
5.卖币:在买/卖交易区进行一键卖币,或通过币币交易卖币。
确认收款后,输入资金密码完成交易。
6.安全设置:为了保障账户安全,建议设置交易密码和绑定谷歌验证器等。
7.查询资产和交易记录:在App中可以查看数字资产余额和历史交易记录。
tp钱包是tp交易所的官方手机客户端,提供多种数字资产的交易服务,并具最好的安全性和稳定性,为你的数字货币交易提供更好的保驾护航功能,让你更加安心的使用tp钱包。
TokenPocket钱包苹果版在安全性方面表现出色。
多层加密技术来确保用户交易本金和个人信息的安全。
TokenPocket钱包还实施了高强度的SSL加密技术和身份验证等,
以及谷歌验证码等,以防止账户盗用和保障交易资金的安全。
在可靠性方面,欧意APP提供了稳定的运行和全面的功能,
包括实时消息推送和个性化设置等。
它还拥有专业的客服团队,提供24小时全天候在线客服支持,
无论是数字资产新手还是专家,都能满足他们的需求